Skip to contents

EAF Calculations

Source: vignettes/EAF.Rmd
EAF.Rmd
library(dplyr)
#> Error in get(paste0(generic, ".", class), envir = get_method_env()) : 
#>   object 'type_sum.accel' not found
library(ggplot2)
library(patchwork)
library(qSIP2)
packageVersion("qSIP2")
#> [1] '0.18.4.9000'

Background

After your qsip_data object has been filtered and resampled, the last step is to calculate the excess atom fraction (EAF) values for each feature. The EAF is a measure of the proportion of a feature that is derived from the labeled substrate. For each of the resamples, the run_EAF_calculations() runs equations from Hungate et al. 20151 to calculate EAF values, and the summarize_EAF_values() function calculates the mean and confidence intervals for each feature.

Getting EAF values

We can start by making a qsip_data object with multiple comparisons using code from the vignette("multiple_objects) vignette. This will make two comparisons (“Normal” and “Drought”) that include the output from run_EAF_calculations().

qsip_list = show_comparison_groups(example_qsip_object, group = "Moisture") |> 
  dplyr::select("group" = Moisture, "unlabeled" = "12C", "labeled" = "13C") |>
  run_comparison_groups(example_qsip_object, 
                        seed = 99,
                        allow_failures = TRUE)
#> Finished groups ■■■■■■■■■■■■■■■■                  50%
#> Finished groups ■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■  100%
#>

Plotting

Plotting the results shows a wide range of EAF values between the two comparisons.

plot_EAF_values(qsip_list)
#> Confidence level = 0.9

The 90% confidence interval is calculated by default, but this can be modified and added to the plot with the confidence and error arguments.

plot_EAF_values(qsip_list, 
                confidence = 0.95, 
                error = "ribbon",
                title = "95% CI")
#> Confidence level = 0.95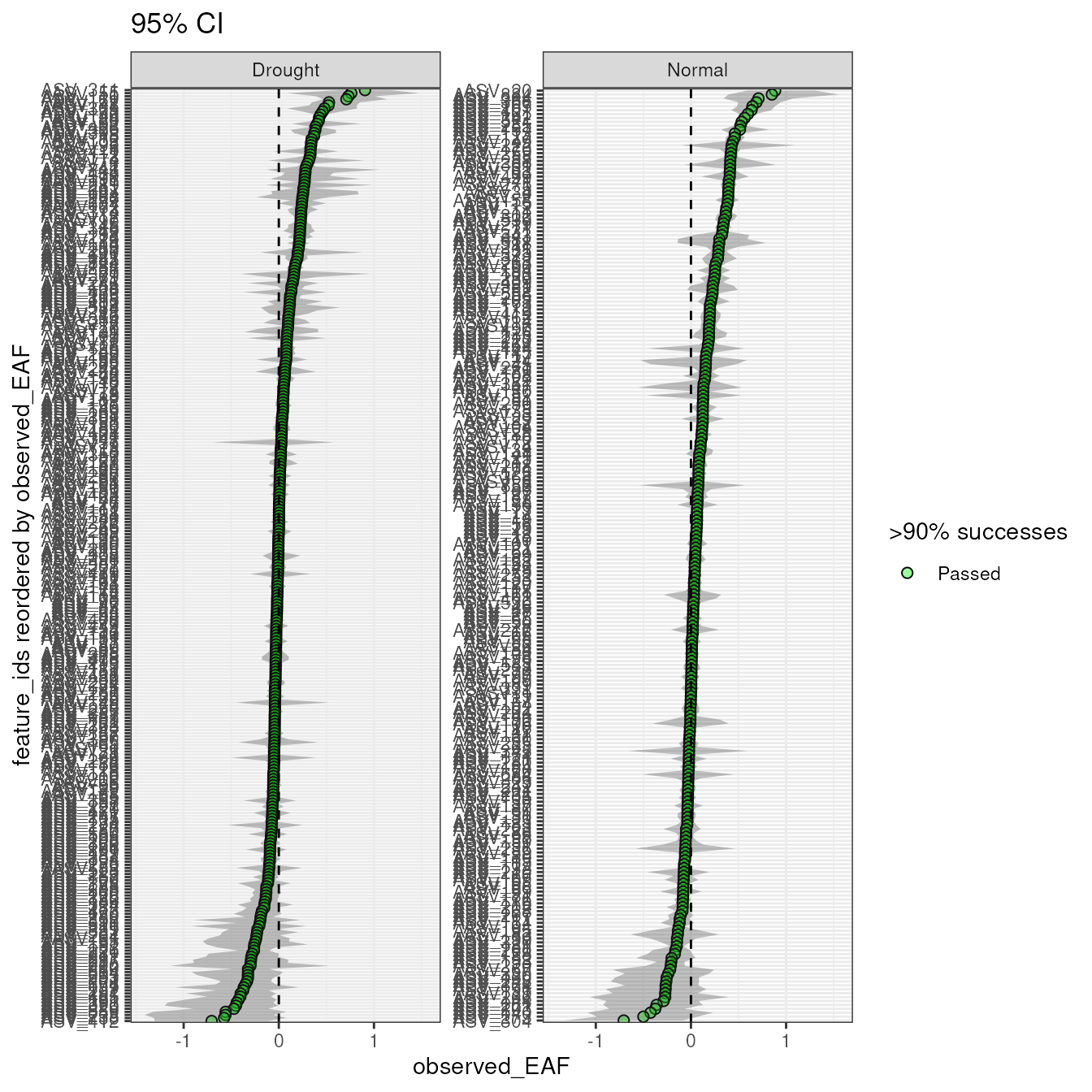

The number of features can be filtered to include the n with the highest EAF.

plot_EAF_values(qsip_list, 
                top = 50, 
                error = "bar",
                title = "95% CI")
#> Confidence level = 0.9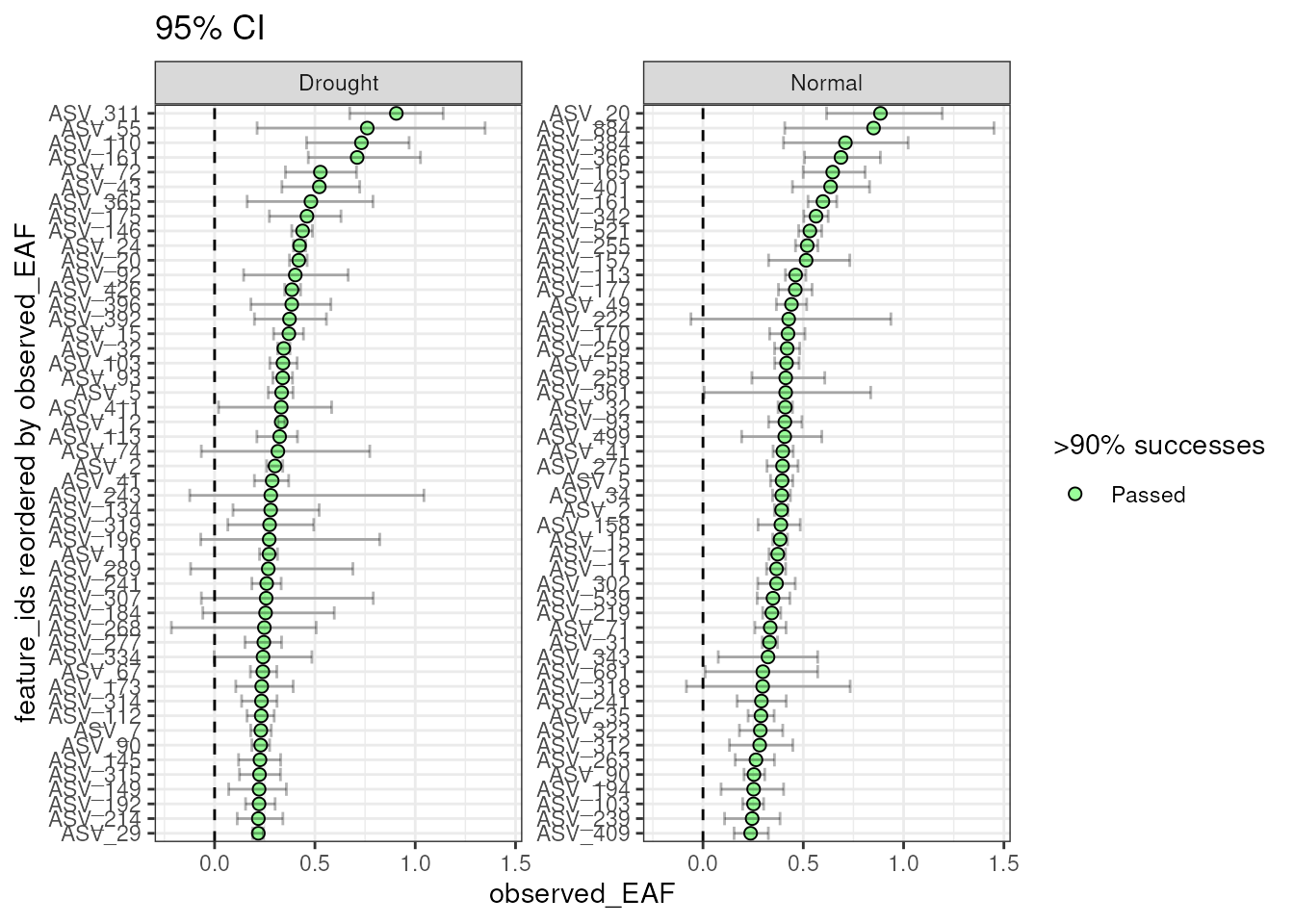

By default, the facets do not share the same y-axis so each comparison are sorted from highto low independently. But, if you want to compare the EAF values between the two comparisons, you can set shared_y = TRUE. Keep in mind that the top n is calculated for each, so you may end up with more than n features in the plot if there isn’t much overlap between the two comparisons.

plot_EAF_values(qsip_list, 
                top = 50,
                shared_y = TRUE,
                error = "bar",
                title = "Y-axis shared for both comparisons")
#> Warning: When setting <shared_y> to TRUE and also passing a value to <top>,
#> there will likely be missing data in the plots if a feature is in the top n of
#> one comparison, but not in the other.
#> Confidence level = 0.9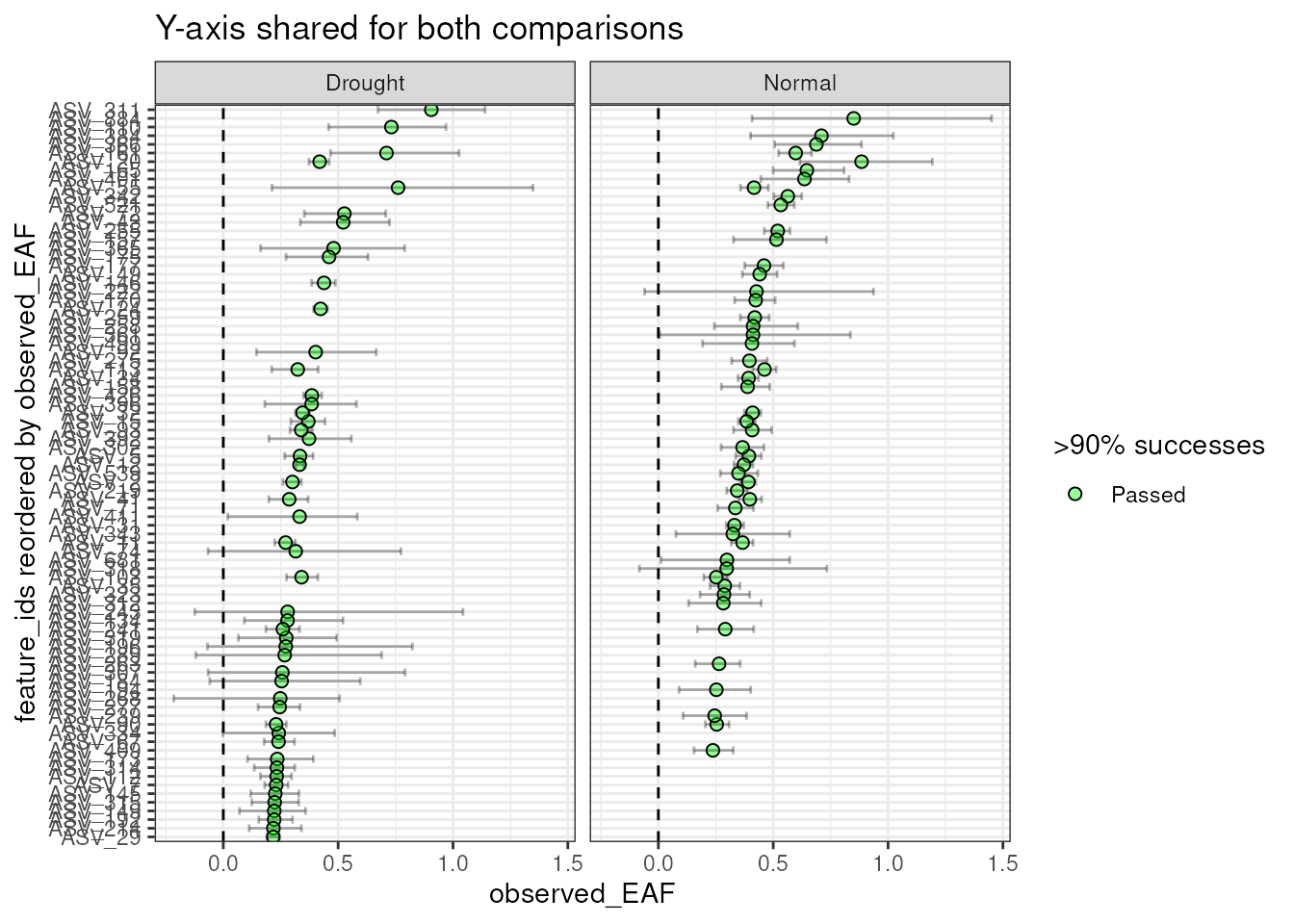

As seen in the warning above, a current limitation when using shared_y = TRUE together with the top argument is that only the top n will be shown per facet, giving a blank value for any features that are not in the top n for that comparison. But, this doesn’t mean they don’t have EAF values or that the feature was not found. I hope to fix this limitation in the future.

As a reminder from the resampling vignette, the “successess” in the legend and colors refer to whether the resampling was successful above a certain threshold. The plot will display whether they pass/fail if the allow_failures argument is set to TRUE in the resampling step.

Dataframe

You can also return the results as a dataframe using summarize_EAF_values() and a desired confidence (default is 90%).

#> Confidence level = 0.9
The first few lines of output
group feature_id observed_EAF mean_resampled_EAF lower upper labeled_resamples unlabeled_resamples labeled_sources unlabeled_sources
Drought ASV_1 -0.0491540 -0.0483554 -0.1082032 0.0087336 1000 1000 4 4
Normal ASV_1 0.0004555 0.0000135 -0.0325729 0.0356580 1000 1000 3 4
Drought ASV_10 0.0547586 0.0550897 0.0344674 0.0747572 1000 1000 4 4
Normal ASV_10 0.1121811 0.1116458 0.0713690 0.1506676 1000 1000 3 4
Drought ASV_100 -0.1116096 -0.1110421 -0.1681262 -0.0503753 1000 1000 4 4
Normal ASV_100 0.0090370 0.0088377 -0.0523892 0.0703022 1000 1000 3 4

More details

Individual features can be inspected further to help understand why their EAF values were calculated as they were. As an example, we will pick 4 features that had a range of EAF values for the “Drought” comparison, one each with high, medium, low, and negative EAF values.

features = c("ASV_72", "ASV_7", "ASV_180", "ASV_100")

summarize_EAF_values(qsip_list$Drought) |>
  filter(feature_id %in% features)
#> Confidence level = 0.9
EAF results for 4 chosen features
feature_id observed_EAF mean_resampled_EAF lower upper labeled_resamples unlabeled_resamples labeled_sources unlabeled_sources
ASV_72 0.5271129 0.5246305 0.3529541 0.7072885 1000 1000 4 4
ASV_7 0.2305506 0.2307068 0.1799998 0.2823904 1000 1000 4 4
ASV_180 0.0308346 0.0318743 -0.0425104 0.0994295 1000 1000 4 4
ASV_100 -0.1116096 -0.1110421 -0.1681262 -0.0503753 1000 1000 4 4

Using a combination of plot_feature_curves() and plot_feature_resamplings() we can plot these 4 features (with some help from the patchwork library).

a = plot_feature_curves(qsip_list$Drought, features) + facet_wrap(~feature_id, nrow = 1, scales = "free")
b = plot_feature_resamplings(qsip_list$Drought, features, intervals = "bar", confidence = 0.95) + facet_wrap(~feature_id, nrow = 1, scales = "free")
(a / b) + 
  plot_layout(axes = "collect") +
  plot_annotation(tag_levels = 'A')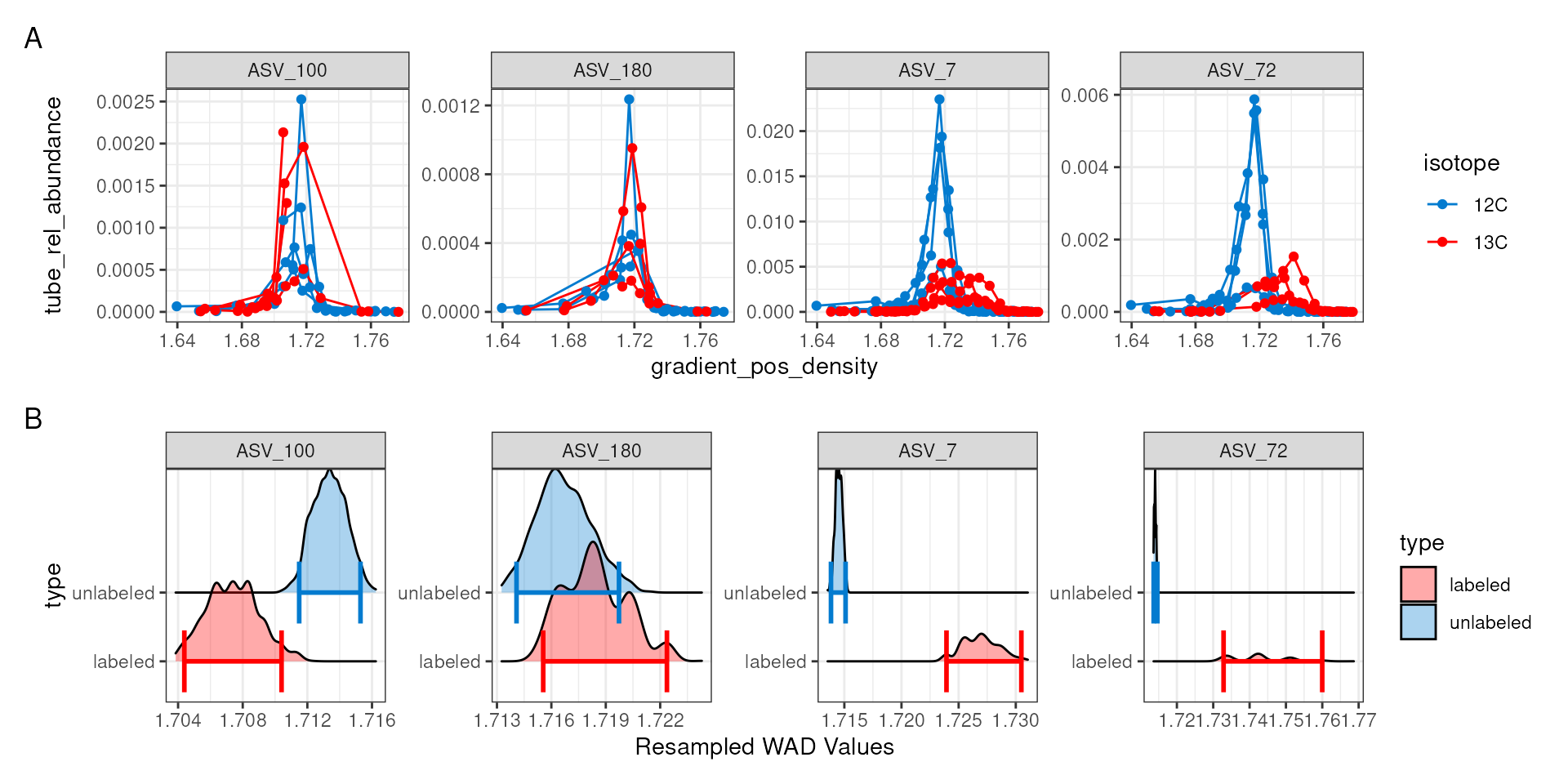

For ASV_7 and ASV_72, it is clear in “A” that the 13C labeled isotope has a nice shift compared to the unlabeled 12C sources. Indeed, the resampling results summarized in “B” also show a clear distinction with non-overlapping confidence intervals. ASV_180, which had an EAF value close to zero shows a much smaller density shift between the unlabeled and labeled samples, and the resampling results show overlapping confidence intervals.

ASV_100, on the other hand, shows a negative EAF value. In “A” we can see the peaks of the 13C do appear shifted left of the 12C, and although the confidence intervals do not overlap, we don’t expect to see lower 13C density values compared to 12C. In “A”, it appears two of the 13C lines abruptly end, which may be a sign that ASV_100 doesn’t occur in as many fractions as necessary.

The plot_feature_occurrence() function can be used to see how often a feature occurs in the samples and give some idea about whether they span the range of densities, are found in fractions close or far from one another, and how the calculated WAD value is affected by these occurrences.

plot_feature_occurrence(qsip_list$Drought, features)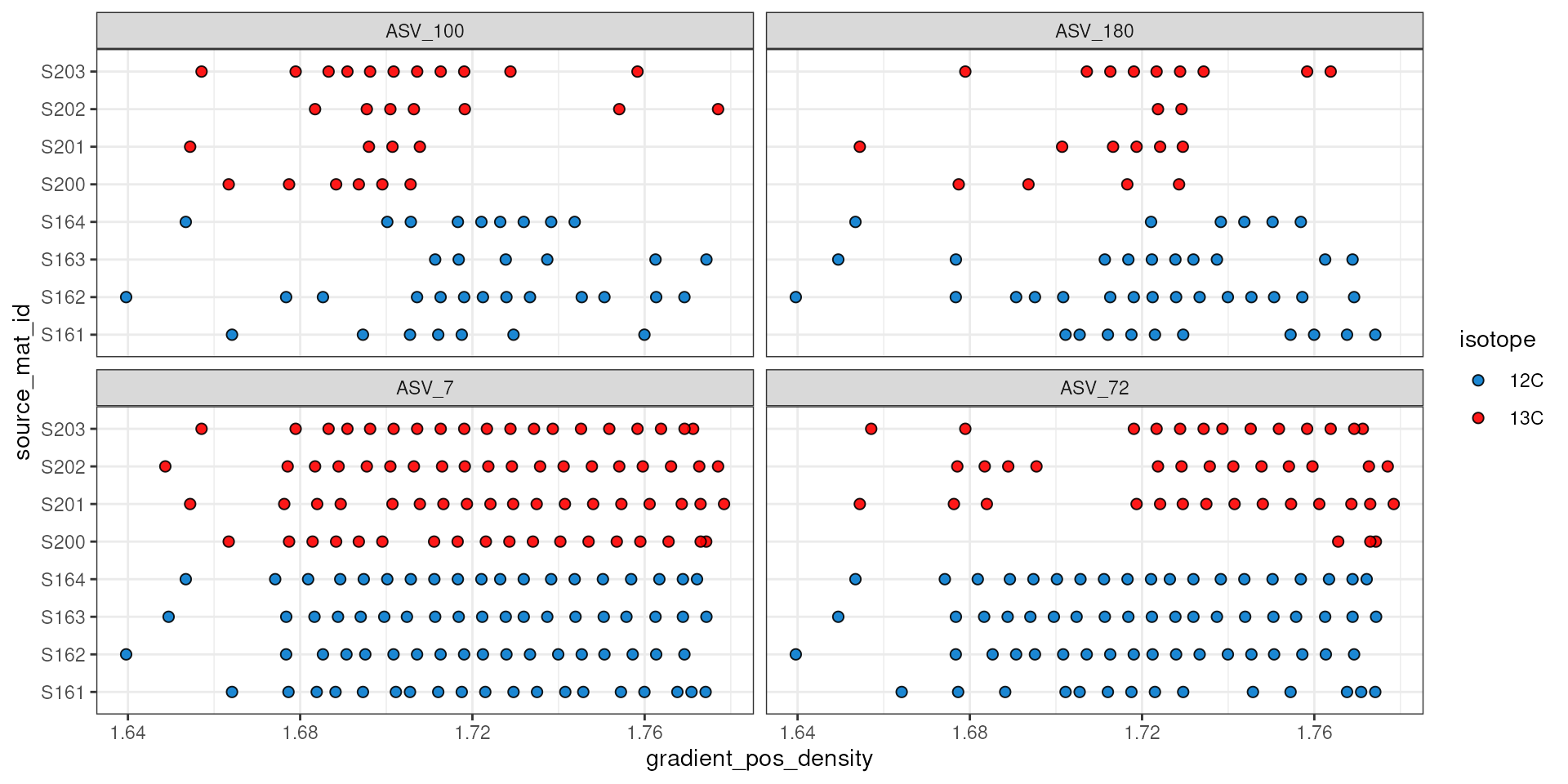

The plot above does show that ASV_100 stops appearing in some labeled sources after a density of ~1.7. With more arguments we can add the WAD and relative abundance values to the make the following figure. Here, the size of the circle represents the relative abundance of the feature in the sample, and for ASV_100 we see the most abundant fraction does heavily influence the calculated WAD value (vertical bar). So, although missing data on the “right side” of the curve may lead to issues, it doesn’t seem to affect the WAD value for ASV_100, assuming the peak of the values are in that most abundant fraction.

plot_feature_occurrence(qsip_list$Drought, 
                        features,
                        show_wad = TRUE,
                        scale = "source")

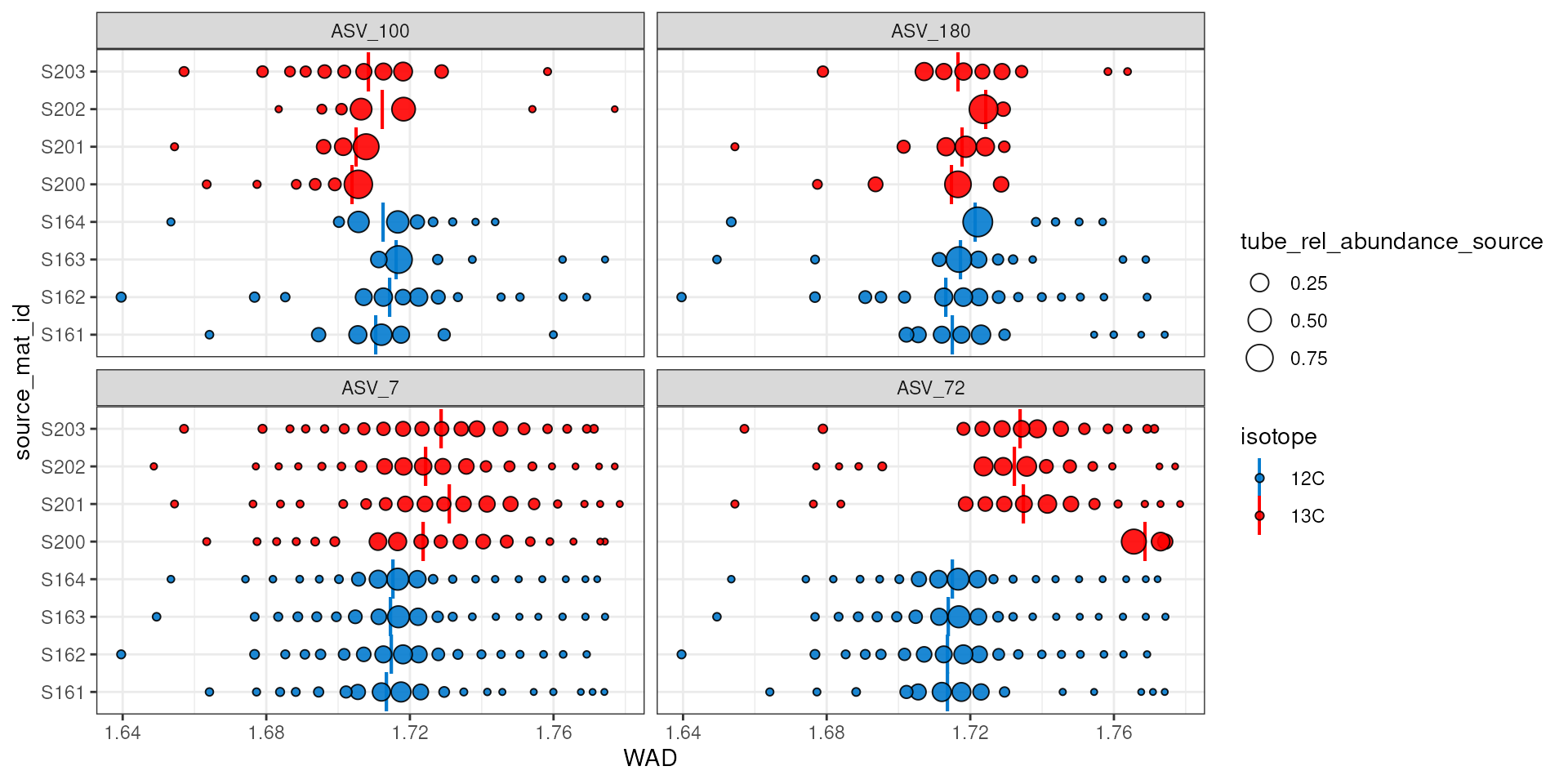
The above plot can also help identify additional potential issues. For example, ASV_72 was one of the features with the highest EAF values, but it looks like source S200 only has it in the extremely heavy fractions, and it has a calculated WAD that is much higher than the other 13C sources. When we ran run_comparison_groups() at the very beginning we didn’t define a minimum number of fractions, so the default of 2 was used. We might, however, consider increasing the minimum number of labeled fractions required to remove sources with feature occurrences like ASV_72 in source S200.